Proofs
CSE 16: Applied Discrete Mathematics
Instructor: Owen Arden
Winter 2023
Proofs
Informal proofs are very common in many disciplines, including math and computer science.

- More than one rule of inference are often used in one step
- Some steps may be skipped
- Which rules of inference and statemenments are used in a step may not be explicitly stated
Proofs
Informal proofs are very common in many disciplines, including math and computer science.

An advantage of this informal style is it may be easier to explain and highlight the less obvious parts of the proof.
Disadvantages of this style are
- Harder to understand without more formal methods experience
- Easier to introduce errors!
A sneaky proof
Here is a proof that for two real numbers \(a\) and \(b\) \(a=b\) implies \(1=2\).
Can you spot the invalid step?
Step
- \(a=b\)
- \(a^2 = a \times b\)
- \(a^2 - b^2 = a \times b - b^2\)
- \((a - b)(a + b) = b(a - b)\)
- \((a + b) = b\)
- \(2b = b\)
- \(2 = 1\)
Reason
- Premise
- Multiply both sides of (1) by \(a\)
- Subtract \(b^2\) from both sides of (2)
- Algebraic equivalence on (3)
- Divide both sides of (4) by \(a-b\)
- Replace \(a\) with \(b\) in (5) since \(a=b\)
- Divide both sides of (6) by \(b\)
Solution: Step 5 divides by 0 since \(a-b=0\) by the premise.
Proofs: the easy parts
Trivial proofs
Vacuous proofs
Counterexamples
Existence proofs
Proving conditionals
Trivial proof: If \(q\) is true, then so is \(p \to q\).
- Example: If it is raining then \(1=1\).
Vacuous proof: If \(p\) is false, then \(p \to q\) is true.
- Example: If unicorns are real then \(2+2=5\).
Counterexamples
Recall \(\neg \forall x. P(x) \equiv \exists x. \neg P(x)\)
To prove \(\neg \forall x. P(x)\), we just need to find a \(c\) such that \(\neg P(c)\).
\(c\) is called a counterexample to the assertion \(\forall x P(x)\).
Example:
“Every positive integer is the sum of the squares of 3 integers.”
The integer \(7\) is a counterexample—it is not the sum of the squares of 3 integers. Therefore the claim is false.
Existence proofs
For theorems of the form \[\exists x. P(x)\] a constructive existence proof is a witness \(w\) such that \(P(w)\)
Since \(P(w)\), then \(\exists x. P(x)\) is true by Existential Generalization.
Example: Show that there is a positive integer that can be written as the sum of cubes of positive integers in two different ways.
Proof.
Consider \(1729\): \[1729 = 10^3 + 9^3 = 12^3 + 1^3\]
Uniqueness proofs
Theorems that assert the existence of a unique element with a particular property have the form \(\exists ! x. P(x)\)
Uniqueness proofs have two parts:
- Existence: We find an element \(w\) such that \(P(w)\).
- Uniqueness: We show that for any other \(v\), \(v \neq w\) implies \(\neg P(v)\)
Example: Show that for real numbers \(a\) and \(b\) where \(a \neq 0\), there is a unique number \(r\) such that \(a \cdot r + b = 0\).
Solution:
- Existence: Choose \(r = \frac{-b}{a}\). Then \(a \cdot (\frac{-b}{a}) + b = -b + b = 0\).
- Uniqueness: Suppose \(s\) is a real number such that \(a \cdot s + b = 0\). Then \(a \cdot s + b = a \cdot r + b\) and therefore: \[\begin{align} a \cdot s + b &= a \cdot r + b \\ a \cdot s &= a \cdot r \\ s &= r \end{align}\]
Allowed assumptions
What can you assume to be true in a proof?
- You can take as given well-known rules and properties of relevant
domains. For example:
- The rules of algebra
- The closure of the integers under arithmetic
- Every integer is either even or odd.
- Sometimes more esoteric properties of a domain should be proven or their proofs referenced.

Remember: proofs are arguments. The goal is to persuade the reader that a statement is true. The easier it is for the reader to understand the truth of the argument, the more persuasive it is.
Premises and previous results
- By definition:
-
A fact known because of a definition.
Example:
“Integer \(m\) is even. By definition, \(m = 2k\) for some integer \(k\).” - By assumption:
-
A fact known because of an assumption.
Example:
“By assumption, \(x\) is positive. Therefore \(x > 0\).”
Direct proofs
- Direct proof:
- A direct proof of a theorem \(p \to c\) assumes \(p\) to be true and proves \(c\) as a direct result.
Theorem: If \(n\) is an odd integer, then \(n^2\) is also odd.
Proof.
Assume \(n\) is odd. By definition, \(n=2k + 1\) for an integer \(k\). Squaring both sides, we get: \[n^2=(2k+1)^2= 4k^2+4k+1=2(2k^2+2k)+1 =
2*r+1\] where \(r=2k^2+2k\) is
an integer. Therefore \(n^2\) is odd.
\(\square\)
\(\square\) marks the end of a proof. Q.E.D. is also used sometimes, an abbreviation of quod erat demonstrandum, latin for “which was to be shown.”
Indirect proofs
Indirect proofs work by proving an alternative theorem that implies the main theorem is true.
Proof by contrapositive
Proof by contradiction
Proof by Contrapositive
Recall that the contrapositive of \(p \to q\) is \(\neg q \to \neg p\) and that \[p \to q \equiv \neg q \to \neg p\]
- Proof by Contrapositive:
- A proof by contrapositive proves a conditional theorem of the form \(p \to q\) by showing the contrapositive \(\neg q \to \neg p\) is true.
Essentially a direct proof of the contrapositive: assume \(\neg q\) to be true and prove \(\neg p\) as a result.
Theorem: If \(n\) is an integer and \(3n+2\) is odd, then \(n\) is odd.
Proof.
Assume \(n\) is even. By definition, \(n=2k\) for some integer \(k\). Thus: \[3n+2 = 3(2k) + 2 = 6k+2 = 2(3k+1) = 2j\]
for \(j = 3k+1\). Therefore \(3n+2\) is even. Since we have shown that if
\(n\) is even, \(3n+2\) is even, it follows by
contraposition that if \(3n+2\) is odd,
then \(n\) is odd. \(\square\).
Proof by Contradiction
- Proof by Contradiction:
- A proof by contradiction proves a theorem \(p\) by assuming \(\neg p\) and deriving a contradiction \(q \wedge \neg q\).
Since a contradiciton must always be false, the assumption \(\neg p\) must be false (\(\neg \neg p)\), thus \(p\) is true.
Theorem: If you pick 22 consecutive calendar days, at least 4 must fall on the same day of the week.
Proof.
Assume for contradiction that no more
than 3 days fall on the same day. Since there are 7 days in a week, it
must be the case that no more than 21 days were chosen. This contradicts
the assumption that 22 days were chosen. \(\square\)
Contradiction example (ZB Theorem 3.6.1)
Theorem: \(\sqrt 2\) is an irrational nunmber.
Proof.
Assume for contradiction \(\sqrt 2\) is rational. By definition (of
rational numbers) there are two integers \(n\) and \(d\) such that \(\frac{n}{d} = \sqrt 2\) where \(d \neq 0\) and \(n\) and \(d\) relatively prime (share no common
factors). Thus no integer greater than 1 divides \(n\) and \(d\).
Then squaring both sides of the equation gives \(\frac{n^2}{d^2} = 2\) and multiplying both sides by \(d^2\) gives \(2d^2 = n^2\). Since $n^2 is a multiple of \(2\), it must be even. Since the square of an even number is even, \(n\) is also even. Therefore \[2d^2 = n^2 = (2k)^2 = 4k^2\]
Dividing by \(2\) we get \(d^2 = 2k^2\). As before, this implies \(d\) is even. But since \(n\) and \(d\) are both even, they are both divisible by 2, contradicting the assumption that \(n\) and \(d\) are relatively prime. Therefore, \(\sqrt 2\) cannot be rational and must be irrational.\(\square\)
Infinite primes (Euclid ~300 B.C.)
- Prime
- An integer \(n\) is prime if and only if \(n > 1\), and the only positive integers that divide \(n\) are \(1\) and \(n\).
- Composite
- An integer \(n\) is composite if and only if \(n > 1\), and there is an integer \(m\) such that \(1 < m < n\) and \(m\) divides \(n\).
Theorem: There are infinitely many prime numbers.
Infinite primes (Euclid ~300 B.C.)
Theorem: There are infinitely many prime numbers.
Proof.
Assume for contradiction that a finite number of primes exist. Let \(p_n\) be the largest prime, and let the sequence \(2, 3, ..., p_n\) be the list of all primes. Consider \[ r = p_1 \times p_2 \times ... \times p_n + 1 \] and observe that since \(r > p_n\), \(r\) must be composite by our assumption that \(p_n\) is the largest prime. Therefore \(r=qk\) where \(k\) is an integer and \(q\) is a prime that divides \(r\).
Since \(q\) is prime, it must be an element of the sequence \(2, 3, ..., p_n\). Therefore it also divides \(p_1 \times p_2 \times ... \times p_n\). But this implies \(q\) divides \(r - p_1 \times p_2 \times ... \times p_n\), a contradiction since \(r - p_1 \times p_2 \times ... \times p_n = 1\).
Therefore there must be an infinite number of primes. \(\square\)
Even 3-ways
- Even
- An integer \(x\) is even if there is an integer \(k\) such that \(x = 2k\).
- Odd
- An integer \(x\) is odd if there is an integer \(k\) such that \(x = 2k+1\).
- Prove that if \(a\) is even and
\(b\) is even, then \(a+b\) is even.
- Direct proof
- Proof by contrapositive
- Proof by contradiction
Proof. (Direct) Assume \(a\) and \(b\) are even. Then by definition \(a = 2k_a\) and \(b = 2k_b\) for some integers \(k_a\) and \(k_b\). Therefore \(a + b = 2k_a + 2k_b = 2(k_a + k_b)\) where \(k_a + k_b\) is also an integer. Therefore, \(a+b\) is even. \(\square\)
Even 3-ways
- Even
- An integer \(x\) is even if there is an integer \(k\) such that \(x = 2k\).
- Odd
- An integer \(x\) is odd if there is an integer \(k\) such that \(x = 2k+1\).
Proof. (Contrapositive) Assume \(a+b\) is odd. Then by definition \(a + b = 2k + 1\) for some integer \(k\). We want to show that \(a\) and \(b\) are not both even. Formally, \(\neg (a = 2k_a \wedge b = 2k_b)\) for some integers \(k_a\) and \(k_b\). Observe \[\begin{align} a+b &= 2k+1 \\ 2k_a + 2k_b &= 2k+1 \\ 2k_a + 2k_b - 2k &= 1 \\ 2(k_a + k_b - k) &= 1 \end{align}\] which has no solution. Therefore either \(a \neq 2k_a\) or \(b \neq 2k_b\), and \[\neg (a \neq 2k_a) \vee \neg (b \neq 2k_b) = \neg (a = 2k_a \wedge b = 2k_b)\] By the contrapositive, if \(a\) and \(b\) are even, then so is \(a+b\). \(\square\)
Even 3-ways
- Even
- An integer \(x\) is even if there is an integer \(k\) such that \(x = 2k\).
- Odd
- An integer \(x\) is odd if there is an integer \(k\) such that \(x = 2k+1\).
Proof. (Contradiction) Assume for contradiction that \(a+b\) is odd. Since \(a\) and \(b\) are even, \(a = 2k_a\) and \(b = 2k_b\) for some integers \(k_a\) and \(k_b\). Then \(a + b = 2k_a + 2k_b = 2(k_a + k_b)\), which implies \(a+b\) is even, contradicting our assumption. Therefore \(a+b\) must be even.
Proving biconditionals (\(p \leftrightarrow q\))
Example: An integer \(x\) is even if and only if \(x^2\) is even.
Proof. Since \(x\) is an arbitrary integer, we specifically want to prove \[\forall x. (x \text{ is even} \leftrightarrow x^2 \text{ is even})\]
Recall that \(p \leftrightarrow q\) is equivalent to \((p \to q) \wedge (q \to p)\). So we can prove \(p \to q\) and \(q \to p\) separately and then combine them using the conjunction rule to get the desired result.
Prove the “forward” case: \(p \to q\)
In the forward/first case, we need to prove that if \(x\) is even, then \(x^2\) is even. We can do that with a direct proof.
Let \(x\) be an even integer. Then by definition, \(x = 2k\) for some integer \(k\). Then \(x^2 = 4k^2 = 2(2k^2)\), so \(x^2\) is even since it is an integer divisible by \(2\).
(This completes the \(p \to q\) case)
Prove the “reverse” case: \(q \to p\)
In the reverse/backward/other case, we need to prove that if \(x^2\) is even, then \(x\) is even. We can do that with a proof by contraposition.
Assume \(x\) is not even. We want to prove that \(x^2\) is not even also. Then \(x = 2k+1\) for some integer \(k\). Then \[x^2 = (2k+1)^2 = 4k^2+4k+1 = 2(2k^2+2k)+1\] which is also odd since \((2k^2+2k)\) is an integer.
Since \(x\) was chosen arbitarily, by UG we have that for any integer \(x\), \(x\) is even if and only if \(x^2\) is even.
Proof by cases
The previous proof technique showed us that we can split up a conjunction and prove each conjunct separately. Using the equivalence \(p \leftrightarrow q \equiv (p \to q) \wedge (q \to p)\), we rewrote the biconditional as a conjunction and proved each case on its own.
We can follow a similar approach when we need to prove a statement holds as long as one of several premises is true: \[(p_1 \vee p_2 \vee ... \vee p_n) \to q\]
This conditional statement is equivalent to this conjunction: \[(p_1 \to q) \wedge (p_2 \to q) \wedge ... \wedge (p_n \to q)\] so we can prove each case \((p_i \to q)\) separately.
Cases example: max operator
Example: Define \[a\: @\: b \triangleq \left\{\begin{array}{c} a & \text{if } a \geq b \\ b & \text{otherwise}\end{array}\right. \] Show that for any real numbers \(a\), \(b\), and \(c\) \[ (a\: @\: b) \: @\: c = a\: @\: (b \: @\: c)\] (In other words, \(@\) is associative.)
Proof. Let \(a\), \(b\), and \(c\) be arbitrary real numbers. Then one of the following 6 cases must hold.
- \(a \geq b \geq c\)
- \(a \geq c \geq b\)
- \(b \geq a \geq c\)
- \(b \geq c \geq a\)
- \(c \geq a \geq b\)
- \(c \geq b \geq a\)
Cases example: max operator
Case 1: \(a \geq b \geq c\)
For this case, by the definition of \(@\), \[\begin{align} a\: @ \: b =& a \\ a\: @ \: c =& a \\ b\: @ \: c =& b \end{align}\]
Therefore \[ (a\: @\: b) \: @\: c = a = a\: @\: (b \: @\: c)\] so the equality holds for this case.
To complete the proof, we need to prove the equality holds for all 6 cases. Can you do them?
- \(a \geq c \geq b\)
- \(b \geq a \geq c\)
- \(b \geq c \geq a\)
- \(c \geq a \geq b\)
- \(c \geq b \geq a\)
Four color theorem
Some proofs have a lot of cases. The four color theorem states that no more than four colors are needed to color the regions of a map so that no two adjacent regions have the same color.
The first correct proof (Appel and Haken, 1976) had 1,834 cases and was controversial because it required a computer to check them all.
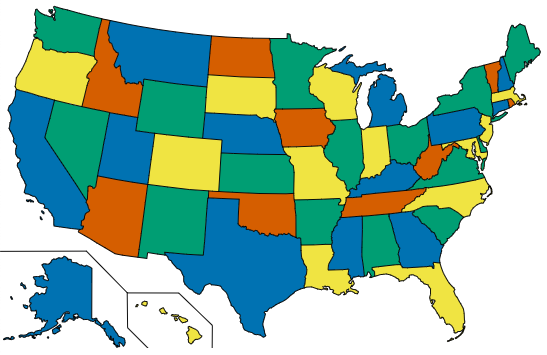
You will prove it in the next homework.
Kidding!